
ABテストを行ってみると、Aの方が良いのか?Bの方が良いのか?甲乙つけがたい結果を得ることが多々あります。本コラムでは、ABテストの結果の信ぴょう性を、偶然率と優位性をもとに判定する計算式『カイ二乗検定』について、実際のやり方を詳しく解説します。
【目次】
1.数値の解釈
2.カイ二乗検定とは?
3.事例・手順
4.優位性が「ない」場合はどうすれば…?
5.まとめ
1.数値の解釈

先日、パートナー企業様との打合せ中、
「ABテストの結果(数値)ってどうやって解釈しているんですか?」
「キャッチコピーのABテストで、CVRが0.03%(←曖昧な結果)上回った方を採用されたことがあって…」
という質問をいただきました。
さて、この判断は正しかったのか?
皆さんならどうやって解釈しますか?
仕事上、様々な前提条件が伴う「数値」と接するのですが、
正直に申し上げますと「伝えたいことありき」の集計・アウトプットになっている資料を目にする機会が少なくありません。
決して穿った見方をしているのではなく、事実確認をすると「それ」とわかってしまうケースがあります。
事業成長に直結する「施策」を選択するためには、
事業成長に直結する「数値」を読み解き、正しく解釈する力が必要です。
2.カイ二乗検定とは?

先ほどの
「ABテストの結果をどうやって解釈しているのか?」
「信ぴょう性をどうやって確認しているのか?」
という質問に対して、
『カイ二乗検定(カイにじょうけんてい)』を利用しています!と回答しました。
【カイ二乗検定とは?】
ネットで調べてみると、「独立性」「分布」「自由度」「帰無仮説」「p値」などなど…。
聞きなれない言葉のオンパレードで、頭がパニックになることかと思います。
ものすごくざっくり説明すると、
ABテストの結果(数値)の信ぴょう性を、『偶然率』と『優位性』をもとに判定する計算式のことです。
● 偶然率:
偶然得られた結果なのか?(今回たまたま得られた結果なのか?)
● 優位性:
意味のある統計結果なのか?(何度やっても同じ結果が得られるのか?)
ABテストの結果を統計的に判定できる便利な計算式、とだけ覚えておけばOKです。
3.事例・手順

では、どのようにして『カイ二乗検定』を行うのか?
大まかな手順は、以下の通りです。
▼ STEP1)
『実測値』の算出
▼ STEP2)
『期待値』の算出
▼ STEP3)
『偶然率』と『優位性』の判定
それでは、実例を用いて、具体的に確認していきましょう。
【STEP1】実測値の算出
『実測値』とは、ABテストで得られた結果(実際の数値)のことです。(※下図参照)
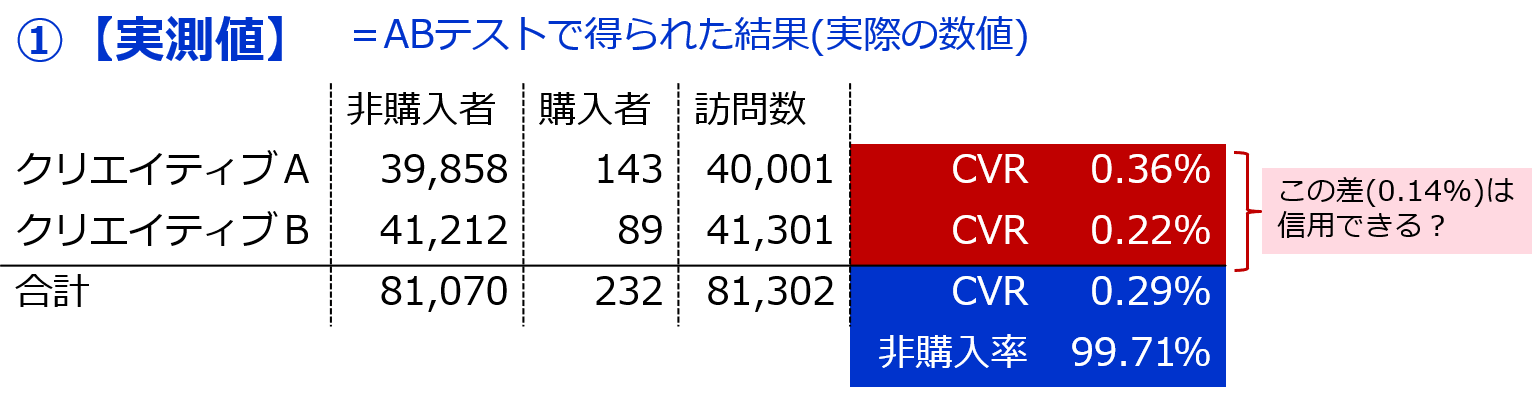
まず始めに、クリエイティブAとBそれぞれの「CVR」を算出します。(※赤色塗りつぶし箇所)
● Aの「CVR」 = 実際の「購入者」143 ÷ 実際の「訪問数」40,001 = 0.36%
● Bの「CVR」 = 実際の「購入者」89 ÷ 実際の「訪問数」41,301 = 0.22%
クリエイティブAとBの「CVR」を比較すると「Aの方が良さそうだ!」となるわけですが、
「この差(0.14%)が本当に信用できるのか?」を判定するのが『カイ二乗検定』です。
次、にAとBを合算した際の「CVR」と「非購入率」を算出します。(※青色塗りつぶし箇所)
● AとBを合算した際の「CVR」 = 実際の「購入者」232 ÷ 実際の「訪問数」81,302 = 0.29%
● 〃 「非購入率」 = 100% - 実際の「購入率(CVR)」0.29% = 99.71%
【STEP2】期待値の算出
『期待値』とは、AとBに差がないと期待した際の数値のことです。(※下図参照)
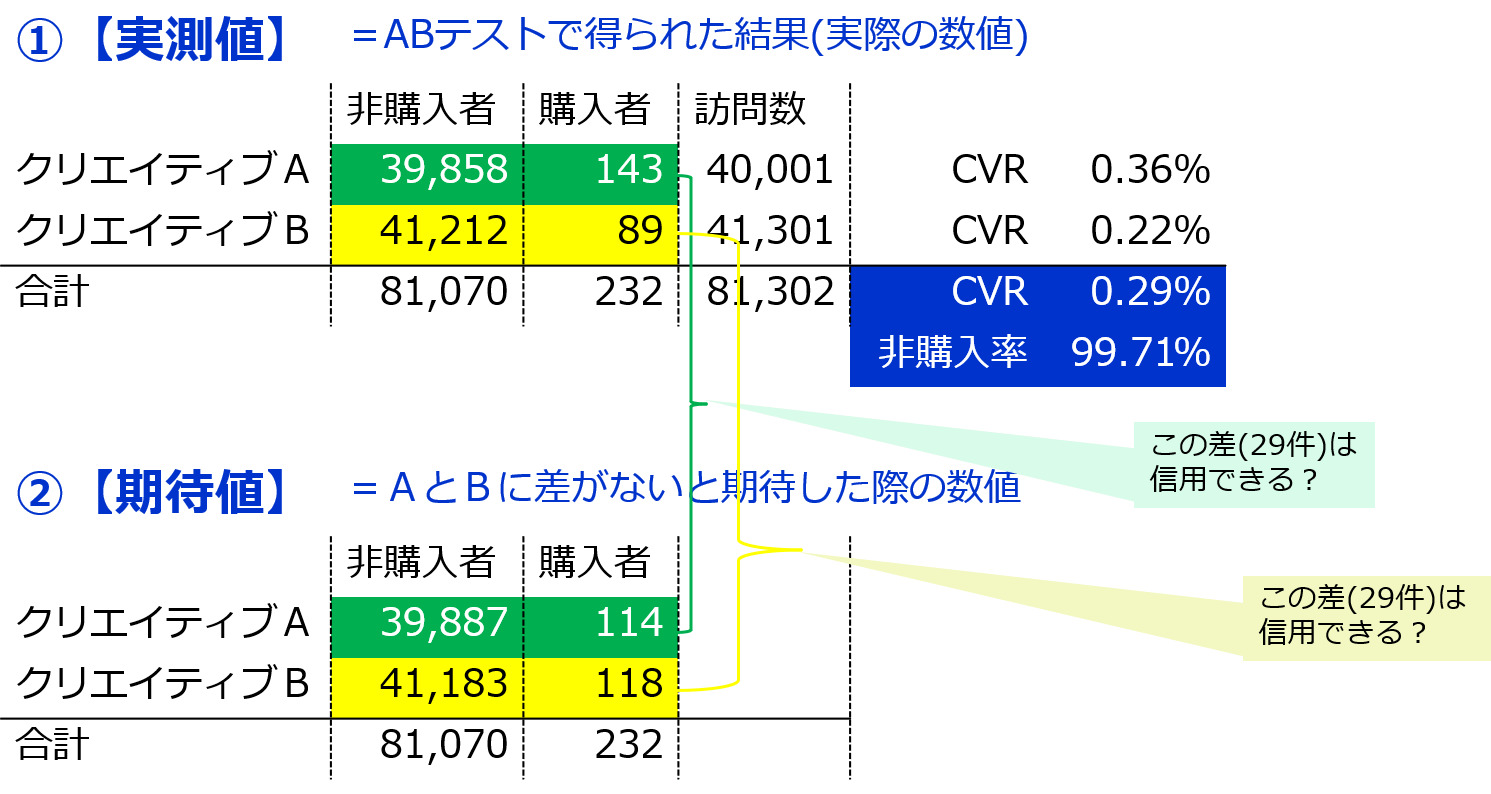
Aについて、以下の『期待値』を算出します。(※緑色塗りつぶし箇所)
● 「非購入者」 = 実際の「訪問者」40,001 × 「非購入率」99.71%* = 39,887
● 「購入者」 = 実際の「訪問者」40,001 × 「CVR」0.29%* = 114
同様に、Bの『期待値』を算出します。(※黄色塗りつぶし箇所)
● 「非購入者」 = 実際の「訪問者」41,301 × 「非購入率」99.71%* = 41,183
● 「購入者」 = 実際の「訪問者」41,301 × 「CVR」0.29%* = 118
*補足:「非購入率」は四捨五入前の【99.7146441661952%】で計算し、「CVR」は四捨五入前の【0.2853558338048%】で計算しています。そのため、図にある四捨五入後の【99.71%】と【0.29%】を使ってお手元で計算すると数字が合わないと思いますが、Excelを利用すれば図と同じ値が算出されるはずです。
ここで、A・Bそれぞれの『実測値』と『期待値』を見比べてみると、
「購入者」も「非購入者」どちらも29件の「差」が生まれていることに気づきます。
この差が「ABテストの差として信用できるのか?」それとも「偶然発生したのか?」を判定するのが『偶然率』になります。
【STEP3】偶然率と優位性の判定
ここで登場するのがExcelの『CHISQ.TEST関数』です。(※下図参照)
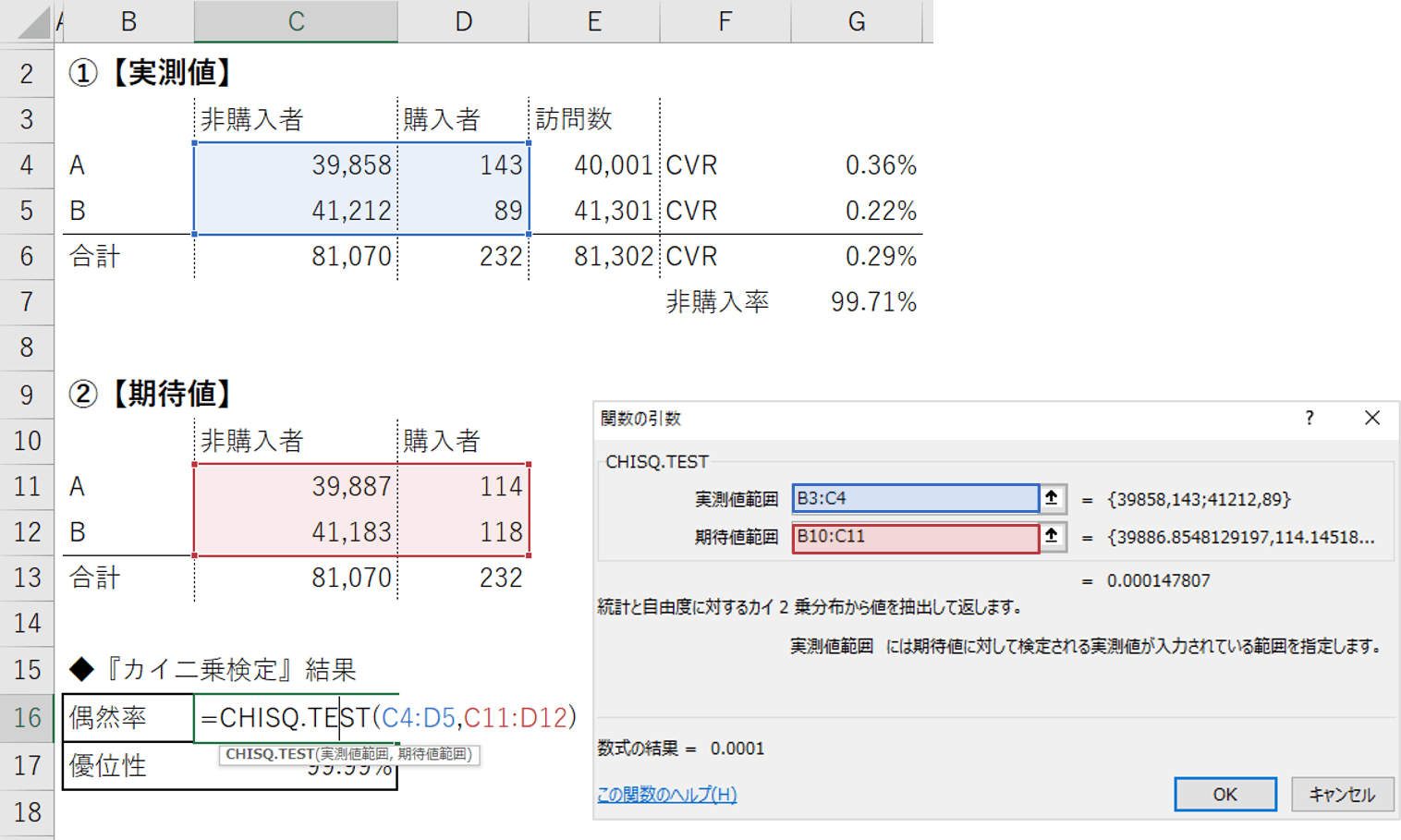
実測値範囲と期待値範囲を指定します。
● 実測値範囲:
『実測値』の、ABそれぞれの「非購入者」と「購入者」(※青色塗りつぶし箇所)
● 期待値範囲:
『期待値』の、ABそれぞれの「非購入者」と「購入者」(※赤色塗りつぶし箇所)
これにより、『カイ二乗検定』を行い、29件の『偶然率』を判定します。
● 『偶然率』が5%未満であれば、
⇒「優位性あり(信用できる意味のある統計結果)」
● 『偶然率』が5%以上であれば、
⇒「優位性なし(たまたま起こった偶然の結果)」と判断します。
今回の事例では、『偶然率』が0.01%となり、「5%」より小さい数値が導き出されたので、
● クリエイティブAとBの「CVR」の差は「優位性あり(信用できる)」
と判断できます。
4.優位性が「ない」場合はどうすれば…?

テスト対象のCVRの差がなんとなく大きく見える場合でも、計算してみると『偶然率』が10%・20%を超える場合、つまり、優位性が「ない」ケースが珍しくありません。
そのようなケースでは、数値が悪いパターンを停止する、という判断になります。
実際の現場では、CVRだけでなく、CTRやCPC、CPOなども含めて総合的に判断すべきですが、
優位性が「ない」場合は、停止すべきクリエイティブを停止する、ということを推奨します。
本来『カイ二乗検定』は、「広告インプレッション数」や「サイト訪問数」などの母数が少ない場合などで起こる「際どい検証結果」の信ぴょう性を判定する際に力を発揮します。
昨今では、Googleを中心とする媒体側のAIによる「配信最適化」や「自動化」が進んでいますが、表面的な数値だけを捉えるのではなく、統計的に計算して「正しく解釈する」ということを、この機会に心掛けてみてはいかがでしょうか?
【簡易ツールのご紹介】
弊社が独自開発した『カイ二乗検定』の簡易ツールを公開しています。
各項目を入力し、検証ボタンをクリックしてください。
※項目は、検証内容に合わせて、以下のように柔軟に解釈してください。
└ 訪問者数:広告インプレッション数、セッション数など
└ 購入者数:クリック数、申込数など
| 検証名 | 訪問者数 | 購入者数 | |
|---|---|---|---|
本コラムでご紹介した実例をもとに優位性を判定すると、以下のようになります。(※下図参照)
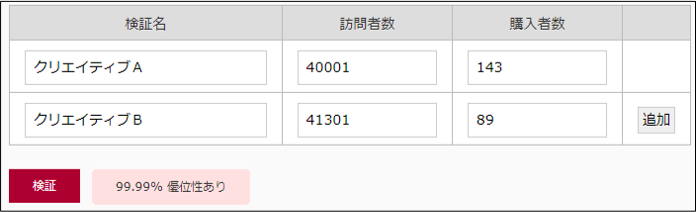
慣れるまでは面倒に感じますが、意外と簡単です。ぜひ、利用してみてください。
5.まとめ

いかがでしたか?最後に、ポイントを整理します。
- ABテストをしてみると、曖昧なテスト結果が出ることが少なくない。
- 結果(数値)の信ぴょう性を統計的に判定できるのが『カイ二乗検定』。
- まずは、『実測値』と『期待値』を算出する。
- その後、Excelの『CHISQ.TEST関数』を利用して、『偶然率』と『優位性』を判定する。
- 『偶然率』が5%未満であれば、『優位性』あり(信用できる意味のある統計結果)と判断する。
以上となります。













